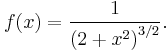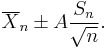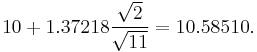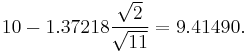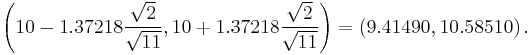Student's t-distribution
Probability density function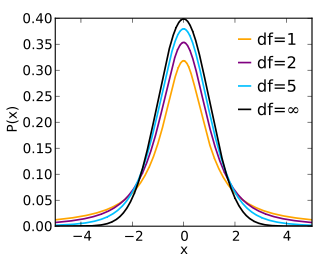 |
|
Cumulative distribution function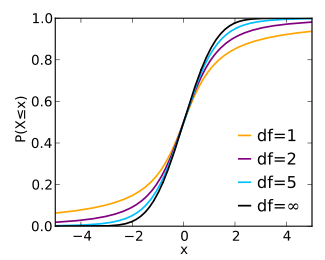 |
|
| parameters: | 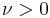 degrees of freedom (real) degrees of freedom (real) |
|---|---|
| support: | 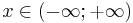 |
| pdf: | 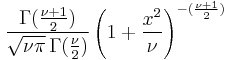 |
| cdf: | ![\begin{matrix}
\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\\[0.5em]
\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};
-\frac{x^2}{\nu} \right)}
{\sqrt{\pi\nu}\,\Gamma (\frac{\nu}{2})}
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ed157c08d8dfcc5459aa89ad6db5f770.png) where 2F1 is the hypergeometric function |
| mean: | 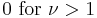 , otherwise undefined , otherwise undefined |
| median: |  |
| mode: | 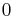 |
| variance: | 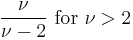 , ,  for for 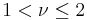 , otherwise undefined , otherwise undefined |
| skewness: | 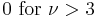 |
| ex.kurtosis: | 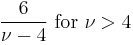 |
| entropy: | ![\begin{matrix}
\frac{\nu+1}{2}\left[
\psi(\frac{1+\nu}{2})
- \psi(\frac{\nu}{2})
\right] \\[0.5em]
+ \log{\left[\sqrt{\nu}B(\frac{\nu}{2},\frac{1}{2})\right]}
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/41353a2518872ce7c9ea9874ac8a243f.png)
|
| mgf: | (Not defined) |
| cf: | 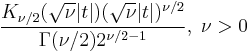
|
In probability and statistics, Student's t-distribution (or simply the t-distribution) is a continuous probability distribution that arises in the problem of estimating the mean of a normally distributed population when the sample size is small. It is the basis of the popular Student's t-tests for the statistical significance of the difference between two sample means, and for confidence intervals for the difference between two population means. The Student's t-distribution also arises in the Bayesian analysis of data from a normal family. The Student's t-distribution is a special case of the generalised hyperbolic distribution.
In statistics, the t-distribution was first derived as a posterior distribution by Helmert and Lüroth.[2][3][4] In the English literature, a derivation of the t-distribution was published in 1908 by William Sealy Gosset[5] while he worked at the Guinness Brewery in Dublin. Due to proprietary issues, the paper was written under the pseudonym Student. The t-test and the associated theory became well-known through the work of R.A. Fisher, who called the distribution "Student's distribution".[6]
Student's distribution arises when (as in nearly all practical statistical work) the population standard deviation is unknown and has to be estimated from the data. Quite often, however, textbook problems will treat the population standard deviation as if it were known and thereby avoid the need to use the Student's t-test. These problems are generally of two kinds: (1) those in which the sample size is so large that one may treat a data-based estimate of the variance as if it were certain, and (2) those that illustrate mathematical reasoning, in which the problem of estimating the standard deviation is temporarily ignored because that is not the point that the author or instructor is then explaining.
Contents |
Etymology
The "Student's" distribution was actually published in 1908 by William Sealy Gosset. Gosset, however, was employed at a brewery that forbade members of its staff publishing scientific papers due to an earlier paper containing trade secrets. To circumvent this restriction, Gosset used the name "Student", and consequently the distribution was named "Student's t-distribution".[7]
Characterization
Student's t-distribution is the probability distribution of the ratio[8]
where
- Z is normally distributed with expected value 0 and variance 1;
- V has a chi-square distribution with
 degrees of freedom;
degrees of freedom; - Z and V are independent.
While, for any given constant μ, 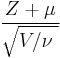 is a random variable of noncentral t-distribution with noncentrality parameter μ.
is a random variable of noncentral t-distribution with noncentrality parameter μ.
Probability density function
Student's t-distribution has the probability density function
where  is the number of degrees of freedom and
is the number of degrees of freedom and  is the Gamma function.
is the Gamma function.
For  even,
even,
For  odd,
odd,
The overall shape of the probability density function of the t-distribution resembles the bell shape of a normally distributed variable with mean 0 and variance 1, except that it is a bit lower and wider. As the number of degrees of freedom grows, the t-distribution approaches the normal distribution with mean 0 and variance 1.
The following images show the density of the t-distribution for increasing values of  . The normal distribution is shown as a blue line for comparison. Note that the t-distribution (red line) becomes closer to the normal distribution as
. The normal distribution is shown as a blue line for comparison. Note that the t-distribution (red line) becomes closer to the normal distribution as  increases.
increases.
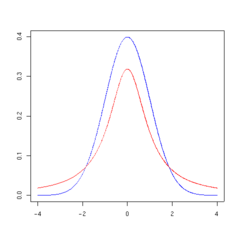
1 degree of freedom
|
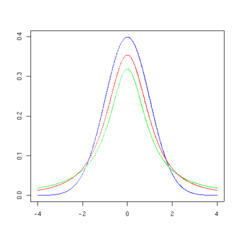
2 degrees of freedom
|
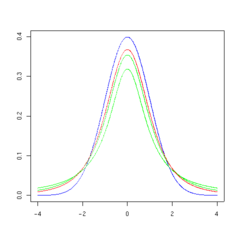
3 degrees of freedom
|
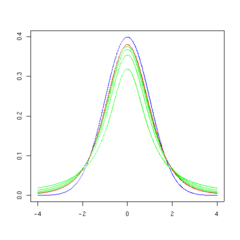
5 degrees of freedom
|
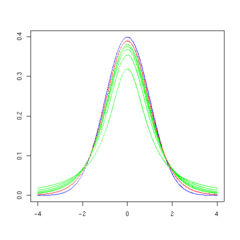
10 degrees of freedom
|
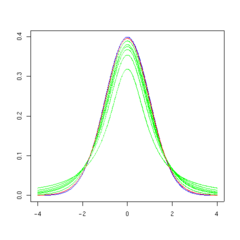
30 degrees of freedom
|
Derivation
Suppose X1, ..., Xn are independent values that are normally distributed with expected value μ and variance σ2. Let
be the sample mean, and
be the sample variance. It can be shown that the random variable
has a chi-square distribution with n − 1 degrees of freedom (by Cochran's theorem). It is readily shown that the quantity
is normally distributed with mean 0 and variance 1, since the sample mean 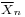 is normally distributed with mean
is normally distributed with mean  and standard error
and standard error 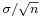 . Moreover, it is possible to show that these two random variables—the normally distributed one and the chi-square-distributed one—are independent. Consequently the pivotal quantity,
. Moreover, it is possible to show that these two random variables—the normally distributed one and the chi-square-distributed one—are independent. Consequently the pivotal quantity,
which differs from Z in that the exact standard deviation 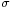 is replaced by the random variable
is replaced by the random variable 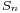 , has a Student's t-distribution as defined above. Notice that the unknown population variance σ2 does not appear in T, since it was in both the numerator and the denominators, so it canceled. Gosset's work showed that T has the probability density function
, has a Student's t-distribution as defined above. Notice that the unknown population variance σ2 does not appear in T, since it was in both the numerator and the denominators, so it canceled. Gosset's work showed that T has the probability density function
with  equal to n − 1.
equal to n − 1.
This may also be written as
where B is the Beta function.
The distribution of T is now called the t-distribution. The parameter  is called the number of degrees of freedom. The distribution depends on
is called the number of degrees of freedom. The distribution depends on  , but not μ or σ; the lack of dependence on μ and σ is what makes the t-distribution important in both theory and practice.
, but not μ or σ; the lack of dependence on μ and σ is what makes the t-distribution important in both theory and practice.
Gosset's result can be stated more generally. (See, for example, Hogg and Craig, Sections 4.4 and 4.8.) Let Z have a normal distribution with mean 0 and variance 1. Let V have a chi-square distribution with  degrees of freedom. Further suppose that Z and V are independent (see Cochran's theorem). Then the ratio
degrees of freedom. Further suppose that Z and V are independent (see Cochran's theorem). Then the ratio
has a t-distribution with  degrees of freedom.
degrees of freedom.
Cumulative distribution function
The cumulative distribution function is given by the regularized incomplete beta function,
with
Properties
Moments
The moments of the t-distribution are
It should be noted that the term for 0 < k <  , k even, may be simplified using the properties of the Gamma function to
, k even, may be simplified using the properties of the Gamma function to
For a t-distribution with  degrees of freedom, the expected value is 0, and its variance is
degrees of freedom, the expected value is 0, and its variance is  /(
/( − 2) if
− 2) if  > 2. The skewness is 0 if
> 2. The skewness is 0 if  > 3 and the excess kurtosis is 6/(
> 3 and the excess kurtosis is 6/( − 4) if
− 4) if  > 4.
> 4.
Confidence intervals
Suppose the number A is so chosen that
when T has a t-distribution with n − 1 degrees of freedom. By symmetry, this is the same as saying that A satisfies
so A is the "95th percentile" of this probability distribution, or 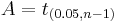 . Then
. Then
and this is equivalent to
Therefore the interval whose endpoints are
is a 90-percent confidence interval for μ. Therefore, if we find the mean of a set of observations that we can reasonably expect to have a normal distribution, we can use the t-distribution to examine whether the confidence limits on that mean include some theoretically predicted value - such as the value predicted on a null hypothesis.
It is this result that is used in the Student's t-tests: since the difference between the means of samples from two normal distributions is itself distributed normally, the t-distribution can be used to examine whether that difference can reasonably be supposed to be zero.
If the data are normally distributed, the one-sided (1 − a)-upper confidence limit (UCL) of the mean, can be calculated using the following equation:
The resulting UCL will be the greatest average value that will occur for a given confidence interval and population size. In other words, 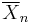 being the mean of the set of observations, the probability that the mean of the distribution is inferior to UCL1−a is equal to the confidence level 1 − a.
being the mean of the set of observations, the probability that the mean of the distribution is inferior to UCL1−a is equal to the confidence level 1 − a.
A number of other statistics can be shown to have t-distributions for samples of moderate size under null hypotheses that are of interest, so that the t-distribution forms the basis for significance tests in other situations as well as when examining the differences between means. For example, the distribution of Spearman's rank correlation coefficient ρ, in the null case (zero correlation) is well approximated by the t distribution for sample sizes above about 20.
Prediction interval
The t-distribution can be used to construct a prediction interval for an unobserved sample from a normal distribution with unknown mean and variance.
Monte Carlo sampling
There are various approaches to constructing random samples from the Student distribution. The matter depends on whether the samples are required on a stand-alone basis, or are to be constructed by application of a quantile function to uniform samples, e.g. in multi-dimensional applications basis on copula-dependency. In the case of stand-alone sampling, Bailey's 1994 extension of the Box-Muller method and its polar variation are easily deployed. It has the merit that it applies equally well to all real positive and negative degrees of freedom.
Integral of Student's probability density function and p-value
The function 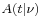 is the integral of Student's probability density function, ƒ(t) between −t and t. It thus gives the probability that a value of t less than that calculated from observed data would occur by chance. Therefore, the function
is the integral of Student's probability density function, ƒ(t) between −t and t. It thus gives the probability that a value of t less than that calculated from observed data would occur by chance. Therefore, the function 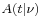 can be used when testing whether the difference between the means of two sets of data is statistically significant, by calculating the corresponding value of t and the probability of its occurrence if the two sets of data were drawn from the same population. This is used in a variety of situations, particularly in t-tests. For the statistic t, with
can be used when testing whether the difference between the means of two sets of data is statistically significant, by calculating the corresponding value of t and the probability of its occurrence if the two sets of data were drawn from the same population. This is used in a variety of situations, particularly in t-tests. For the statistic t, with 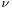 degrees of freedom,
degrees of freedom, 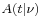 is the probability that t would be less than the observed value if the two means were the same (provided that the smaller mean is subtracted from the larger, so that t > 0). It is defined for real t by the following formula:
is the probability that t would be less than the observed value if the two means were the same (provided that the smaller mean is subtracted from the larger, so that t > 0). It is defined for real t by the following formula:
where B is the Beta function. For t > 0, there is a relation to the regularized incomplete beta function Ix(a, b) as follows:
For statistical hypothesis testing this function is used to construct the p-value.
Related distributions
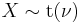 has a t-distribution if
has a t-distribution if 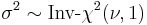 has a scaled inverse-χ2 distribution and
has a scaled inverse-χ2 distribution and 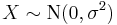 has a normal distribution.
has a normal distribution. has an F-distribution if
has an F-distribution if 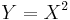 and
and 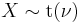 has a Student's t-distribution.
has a Student's t-distribution.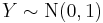 has a normal distribution as
has a normal distribution as 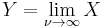 where
where 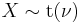 .
.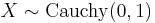 has a Cauchy distribution if
has a Cauchy distribution if 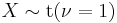 .
.
Special cases
Certain values of  give an especially simple form.
give an especially simple form.
ν = 1
Distribution function:
Density function:
See Cauchy distribution
ν = 2
Distribution function:
Density function:
Occurrences
Hypothesis testing
Confidence intervals and hypothesis tests rely on Student's t-distribution to cope with uncertainty resulting from estimating the standard deviation from a sample, whereas if the population standard deviation were known, a normal distribution would be used.
Robust parametric modeling
The t-distribution is often used as an alternative to the normal distribution as a model for data.[9] It is frequently the case that real data have heavier tails than the normal distribution allows for. The classical approach was to identify outliers and exclude or downweight them in some way. However, it is not always easy to identify outliers (especially in high dimensions), and the t-distribution is a natural choice of model for such data and provides a parametric approach to robust statistics.
Lange et al. explored the use of the t-distribution for robust modeling of heavy tailed data in a variety of contexts. A Bayesian account can be found in Gelman et al. The degrees of freedom parameter controls the kurtosis of the distribution and is correlated with the scale parameter. The likelihood can have multiple local maxima and, as such, it is often necessary to fix the degrees of freedom at a fairly low value and estimate the other parameters taking this as given. Some authors report that values between 3 and 9 are often good choices. Venables and Ripley suggest that a value of 5 is often a good choice.
Table of selected values
Most statistical textbooks list t distribution tables. Nowadays, the better way to a fully precise critical t value or a cumulative probability is the statistical function implemented in spreadsheets (Office Excel, OpenOffice Calc, etc.), or an interactive calculating web page. The relevant spreadsheet functions are TDIST and TINV, while online calculating pages save troubles like positions of parameters or names of functions. For example, a Mediawiki page supported by R extension can easily give the interactive result of critical values or cumulative probability, even for noncentral t-distribution.
The following table lists a few selected values for t-distributions with  degrees of freedom for a range of one-sided or two-sided critical regions. For an example of how to read this table, take the fourth row, which begins with 4; that means
degrees of freedom for a range of one-sided or two-sided critical regions. For an example of how to read this table, take the fourth row, which begins with 4; that means  , the number of degrees of freedom, is 4 (and if we are dealing, as above, with n values with a fixed sum, n = 5). Take the fifth entry, in the column headed 95% for one-sided (90% for two-sided). The value of that entry is "2.132". Then the probability that T is less than 2.132 is 95% or Pr(−∞ < T < 2.132) = 0.95; or mean that Pr(−2.132 < T < 2.132) = 0.9.
, the number of degrees of freedom, is 4 (and if we are dealing, as above, with n values with a fixed sum, n = 5). Take the fifth entry, in the column headed 95% for one-sided (90% for two-sided). The value of that entry is "2.132". Then the probability that T is less than 2.132 is 95% or Pr(−∞ < T < 2.132) = 0.95; or mean that Pr(−2.132 < T < 2.132) = 0.9.
This can be calculated by the symmetry of the distribution,
- Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,
and so
- Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.
Note that the last row also gives critical points: a t-distribution with infinitely-many degrees of freedom is a normal distribution. (See above: Related distributions).
| One Sided | 75% | 80% | 85% | 90% | 95% | 97.5% | 99% | 99.5% | 99.75% | 99.9% | 99.95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Two Sided | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.5% | 99.8% | 99.9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
 |
0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
The number at the beginning of each row in the table above is  which has been defined above as n − 1. The percentage along the top is 100%(1 − α). The numbers in the main body of the table are tα,
which has been defined above as n − 1. The percentage along the top is 100%(1 − α). The numbers in the main body of the table are tα, . If a quantity T is distributed as a Student's t distribution with
. If a quantity T is distributed as a Student's t distribution with  degrees of freedom, then there is a probability 1 − α that T will be less than tα,
degrees of freedom, then there is a probability 1 − α that T will be less than tα, .(Calculated as for a one-tailed or one-sided test as opposed to a two-tailed test.)
.(Calculated as for a one-tailed or one-sided test as opposed to a two-tailed test.)
For example, given a sample with a sample variance 2 and sample mean of 10, taken from a sample set of 11 (10 degrees of freedom), using the formula
We can determine that at 90% confidence, we have a true mean lying below
(In other words, on average, 90% of the times that an upper threshold is calculated by this method, the true mean lies below this upper threshold.) And, still at 90% confidence, we have a true mean lying over
(In other words, on average, 90% of the times that a lower threshold is calculated by this method, the true mean lies above this lower threshold.) So that at 80% confidence, we have a true mean lying within the interval
This is generally expressed in interval notation, e.g., for this case, at 80% confidence the true mean is within the interval [9.41490, 10.58510].
(In other words, on average, 80% of the times that upper and lower thresholds are calculated by this method, the true mean is both below the upper threshold and above the lower threshold. This is not the same thing as saying that there is an 80% probability that the true mean lies between a particular pair of upper and lower thresholds that have been calculated by this method—see confidence interval and prosecutor's fallacy.)
For information on the inverse cumulative distribution function see Quantile function.
See also
- Student's t-statistic
- F-distribution
- Gamma function
- Hotelling's T-square distribution
- Noncentral t-distribution
- Multivariate Student distribution
- Confidence interval
- Variance
Notes
- ↑ Hurst, Simon, The Characteristic Function of the Student-t Distribution, Financial Mathematics Research Report No. FMRR006-95, Statistics Research Report No. SRR044-95
- ↑ Lüroth, J (1876). "Vergleichung von zwei Werten des wahrscheinlichen Fehlers". Astron. Nachr. 87: 209–20.
- ↑ Pfanzagl, J.; Sheynin, O. (1996). "A forerunner of the t-distribution (Studies in the history of probability and statistics XLIV)". Biometrika 83 (4): pp. 891–898. doi:10.1093/biomet/83.4.891. MR1766040. http://biomet.oxfordjournals.org/cgi/content/abstract/83/4/891.
- ↑ Sheynin, O (1995). "Helmert's work in the theory of errors". Arch. Hist. Ex. Sci. 49: 73-104.
- ↑ Student [William Sealy Gosset] (March 1908). "The probable error of a mean". Biometrika 6 (1): 1–25. doi:10.1093/biomet/6.1.1. http://www.york.ac.uk/depts/maths/histstat/student.pdf.
- ↑ Fisher, R. A. (1925). "Applications of "Student's" distribution". Metron 5: 90–104. http://digital.library.adelaide.edu.au/coll/special/fisher/43.pdf.
- ↑ Walpole, Ronald; Myers, Raymond; Ye, Keying. Probability and Statistics for Engineers and Scientists. Pearson Education, 2002, 7th edition, pg. 237
- ↑ Johnson, N.L., Kotz, S., Balakrishnan, N. (1995) Continuous Univariate Distributions, Volume 2, 2nd Edition. Wiley, ISBN 0-471-58494-0 (Chapter 28)
- ↑ Lange, Kenneth L.; Little, Roderick J.A.; Taylor, Jeremy M.G. (1989). "Robust statistical modeling using the t-distribution". JASA 84 (408): 881–896. http://www.jstor.org/stable/2290063.
References
- Helmert, F. R. (1875). Über die Bestimmung des wahrscheinlichen Fehlers aus einer endlichen Anzahl wahrer Beobachtungsfehler. Z. Math. Phys. 20, 300-3.
- Helmert, F. R. (1876a). Über die Wahrscheinlichkeit der Potenzsummen der Beobachtungsfehler und uber einige damit in Zusammenhang stehende Fragen. Z. Math. Phys. 21, 192-218.
- Helmert, F. R. (1876b). Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit Astron. Nachr. 88, 113-32.
- Senn, S. & Richardson, W. (1994). The first t-test. Statist. Med. 13, 785-803.
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 26", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 948, MR0167642, ISBN 978-0486612720, http://www.math.sfu.ca/~cbm/aands/page_948.htm.
- R.V. Hogg and A.T. Craig (1978). Introduction to Mathematical Statistics. New York: Macmillan.
- Press, William H.; Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery (1992). Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press. pp. pp. 228–229. ISBN 0-521-43108-5. http://www.nr.com/.
- Bailey, R. W. (1994). Polar generation of random variates with the t-distribution. Mathematics of Computation 62(206), 779–781.
- W.N. Venables and B.D. Ripley, Modern Applied Statistics with S (Fourth Edition), Springer, 2002
- Gelman, Andrew; John B. Carlin, Hal S. Stern, Donald B. Rubin (2003). Bayesian Data Analysis (Second Edition). CRC/Chapman & Hall. ISBN 1-584-88388-X. http://www.stat.columbia.edu/~gelman/book/.
External links
- Comparison of noncentral and central t-distributions Density plot, critical value, cumulative probability, etc., noncentral t-distribution online calculator, based on R platform embedded in Mediawiki
- VassarStats Density plot, critical values, etc., calculated for a user-specified number of d.f.
- Earliest Known Uses of Some of the Words of Mathematics (S) (Remarks on the history of the term "Student's distribution")
- Cumulative distribution function (CDF) calculator for the Student t-distribution
- Probability density function (PDF) calculator for the Student t-distribution
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 : digamma function,
: digamma function, :
: 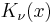 :
: 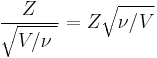
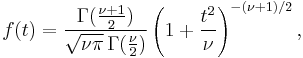
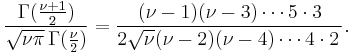
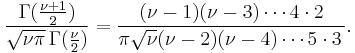
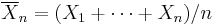
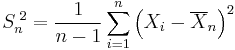
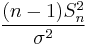
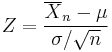
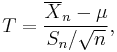
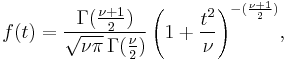
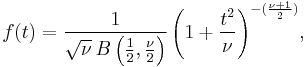
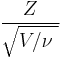
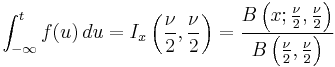
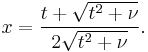
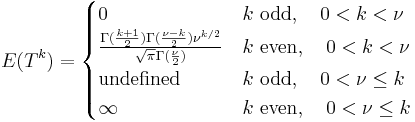
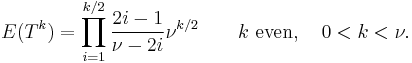
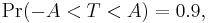
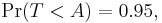
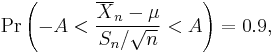
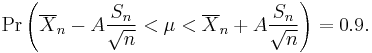
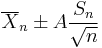
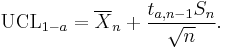
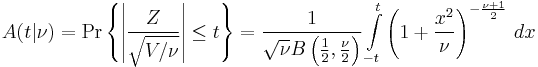
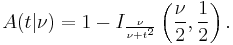
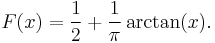
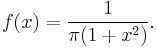
![F(x) = \frac{1}{2}\left[1+\frac{x}{\sqrt{2+x^2}}\right].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/f92fe71ba5acb2a400a941c9d32209a4.png)